Die Formeln und Formen der Erde
Was unseren Planeten so perfekt macht

Die Schönheit der Natur ist kein Zufall. Ihre Formen, Muster und Strukturen folgen bestimmten Regeln.
Die Mathematik ist die Brille, die wir aufsetzen, um den Bauplan der Erde sichtbar zu machen.
Ein Garant für das Überleben vieler Arten ist zum Beispiel die Fibonacci-Folge, benannt nach dem Mathematiker Leonardo Fibonacci.
Was steckt dahinter?

Die Fibonacci-Folge

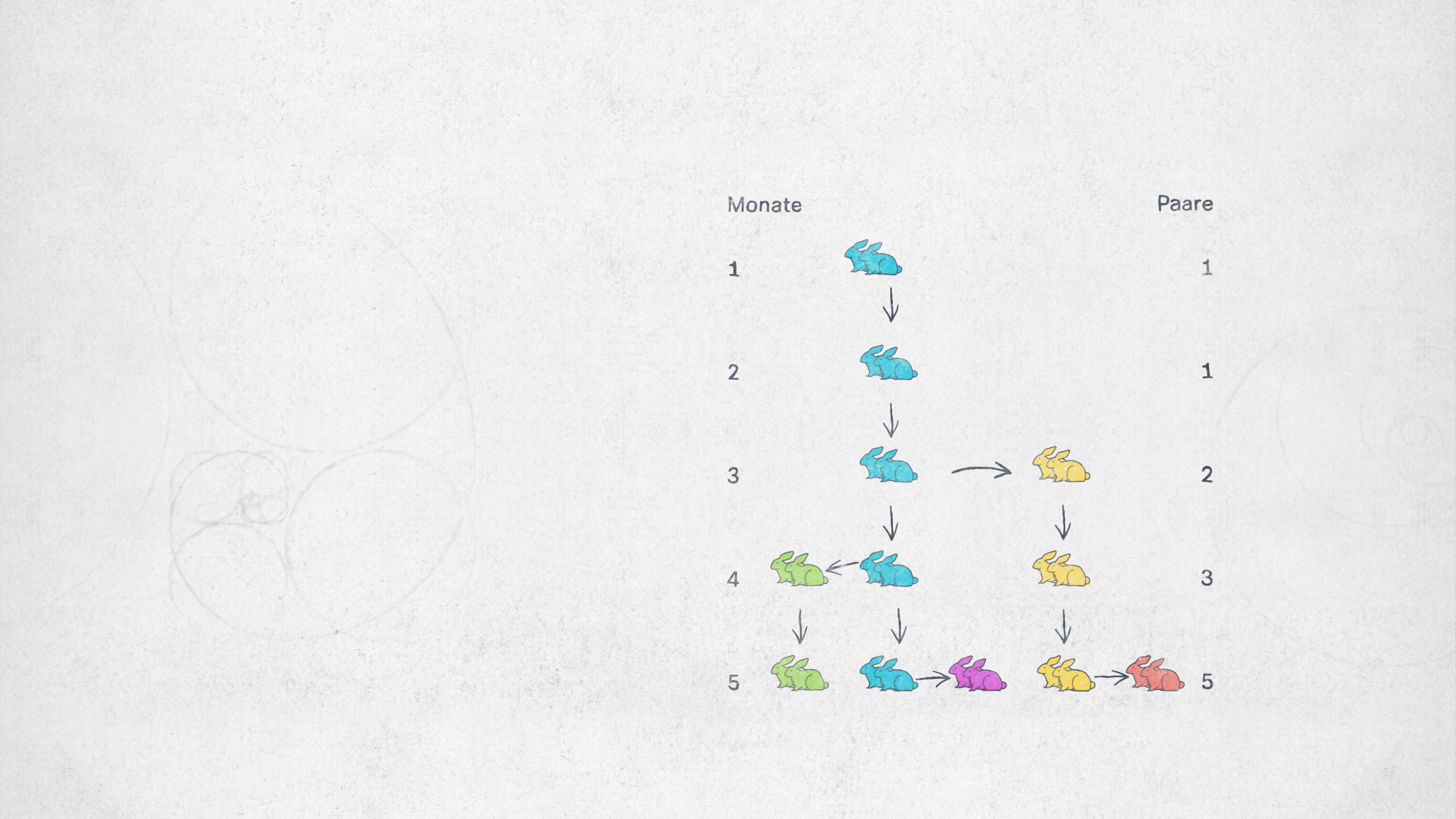


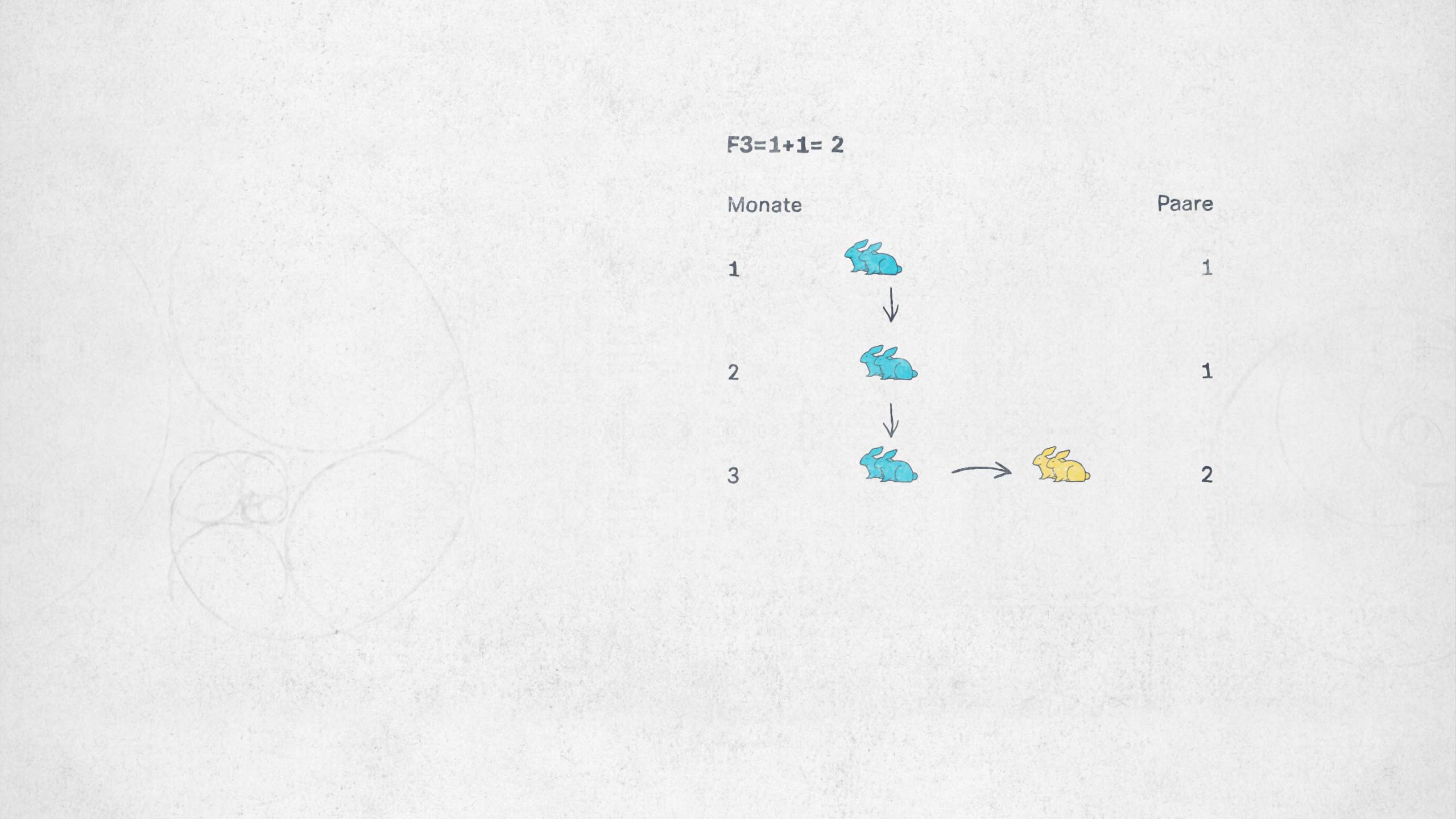
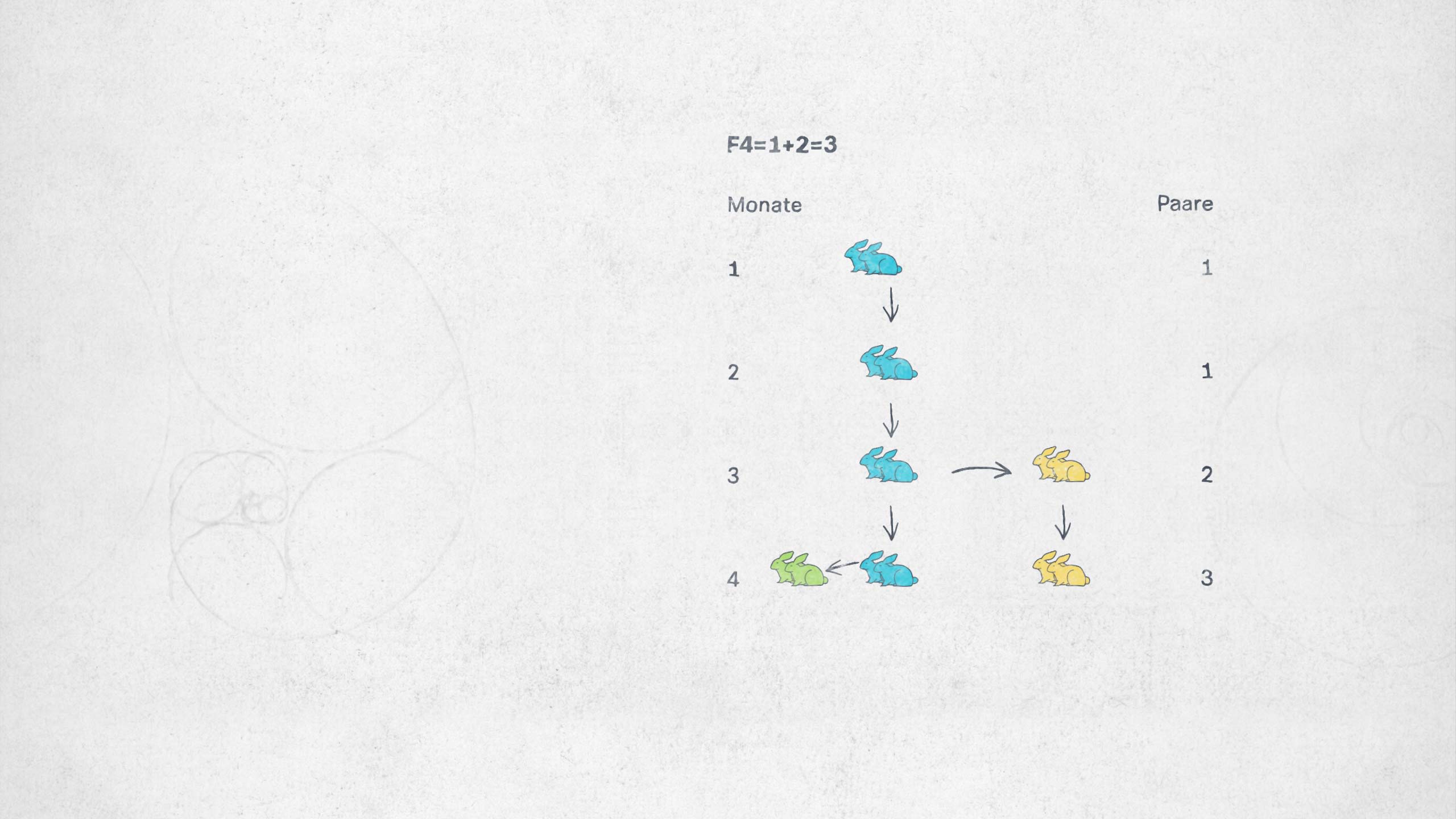
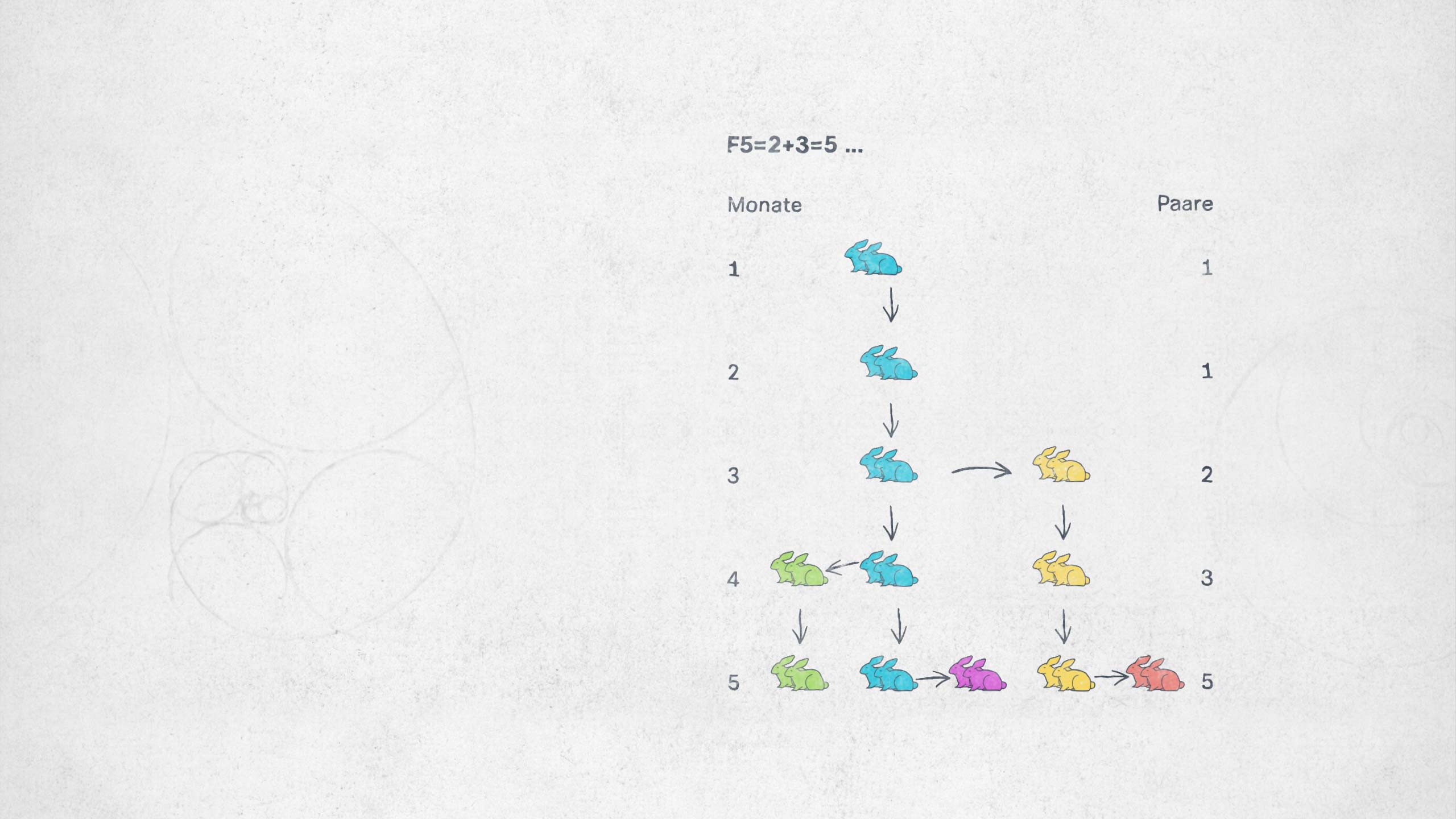

Ursprünglich hat Fibonacci das anhand einer Kaninchenpopulation und deren Wachstum durchgespielt.
Seine theoretische Annahme:
- Jedes Paar bekommt zwei Kinder
- Nachwuchs bekommt nicht direkt Kinder, sondern erst im Monat darauf
Am Anfang gibt es ein Kaninchenpaar, das nach einem Monat geschlechtsreif ist.
Dann bekommt es Nachwuchs, also gibt es nun zwei Paare.
Im nächsten Monat kommt wieder Nachwuchs dazu, also: drei Paare.
Neben dem Elternpaar bekommt nun auch der geschlechtsreife Nachwuchs Kinder, also fünf Paare insgesamt.
Diese theoretische Annahme ergibt die Fibonacci-Folge. Zahlen, die unendlich erweitert werden können.

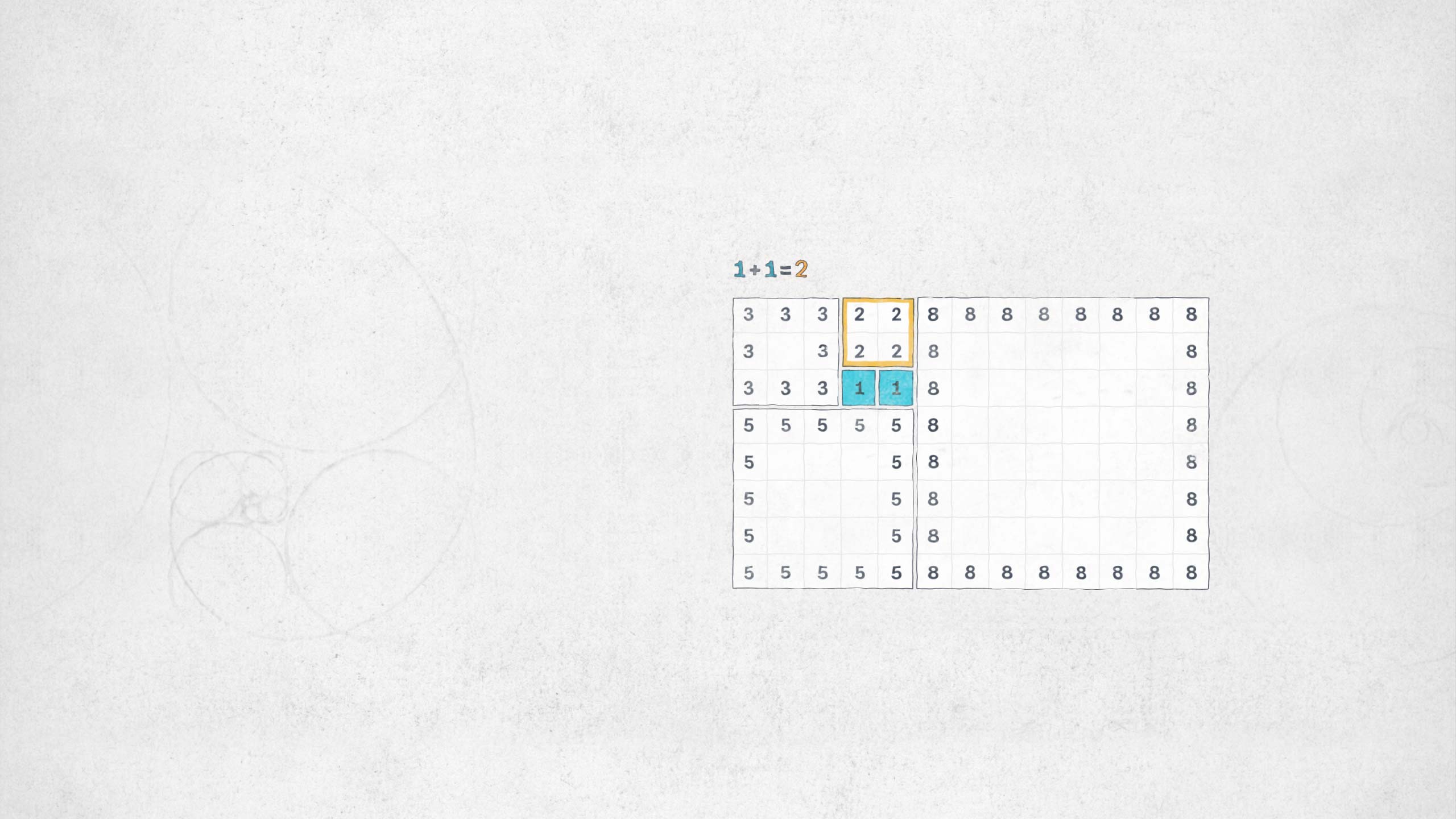
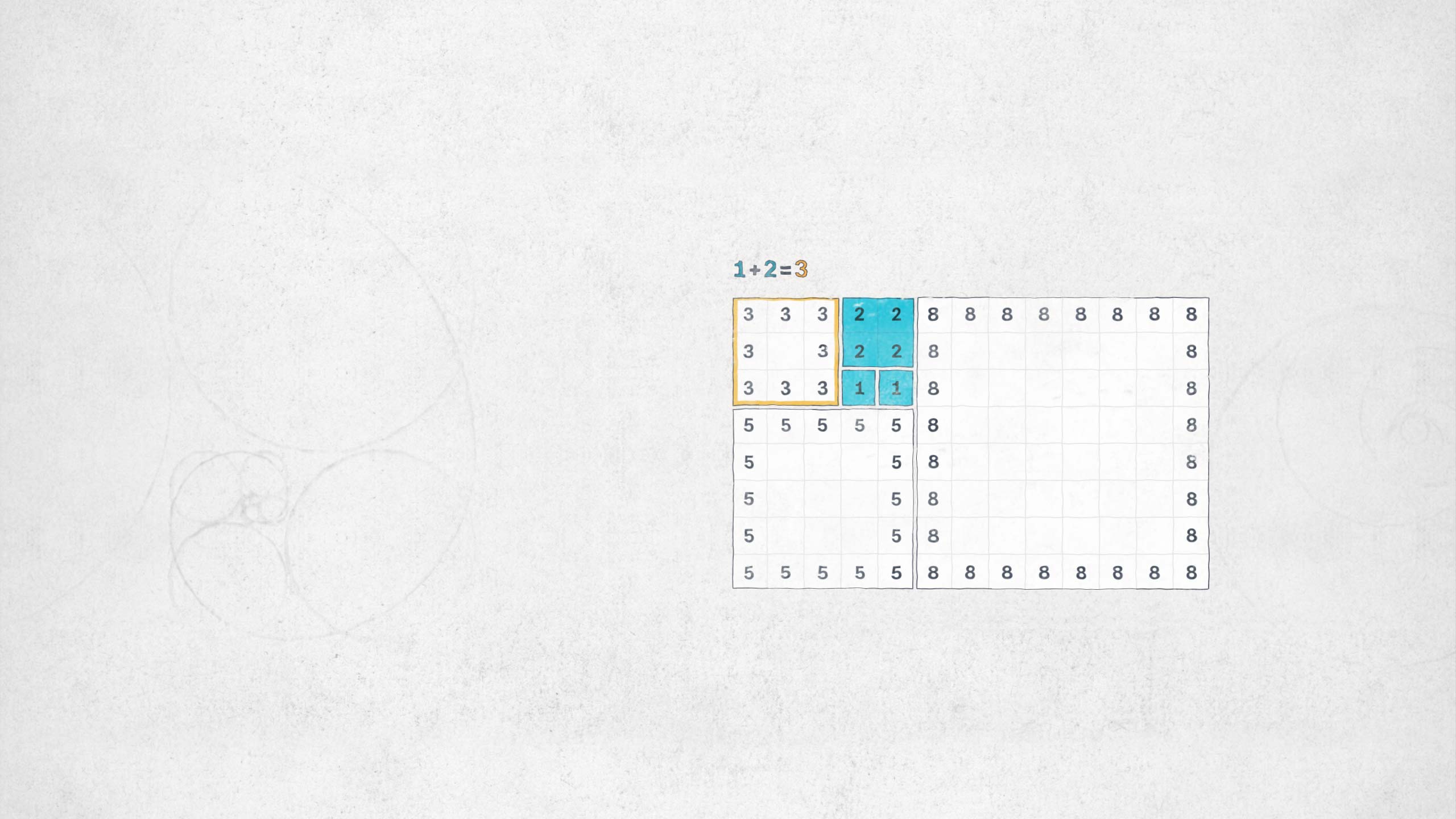
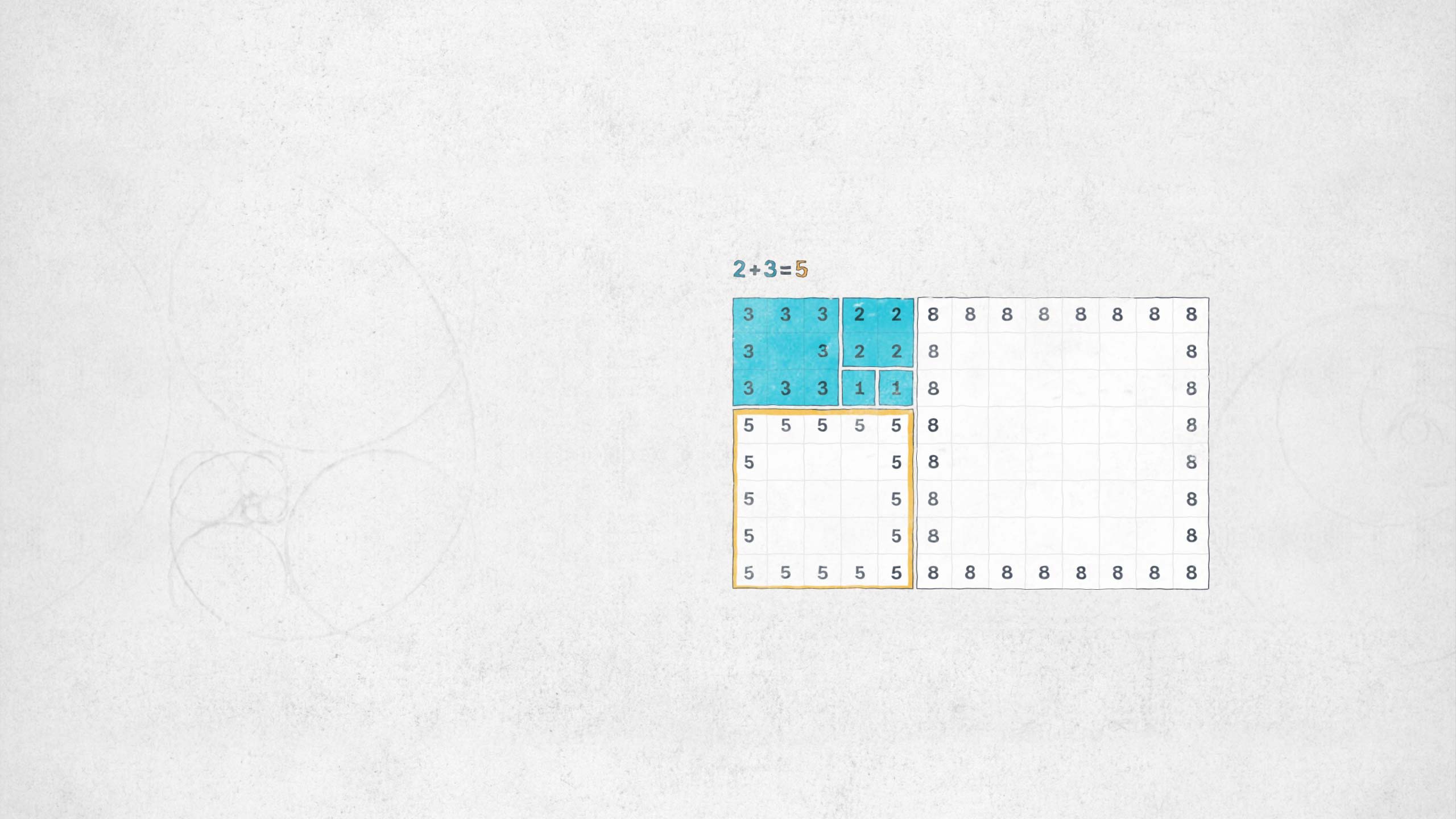
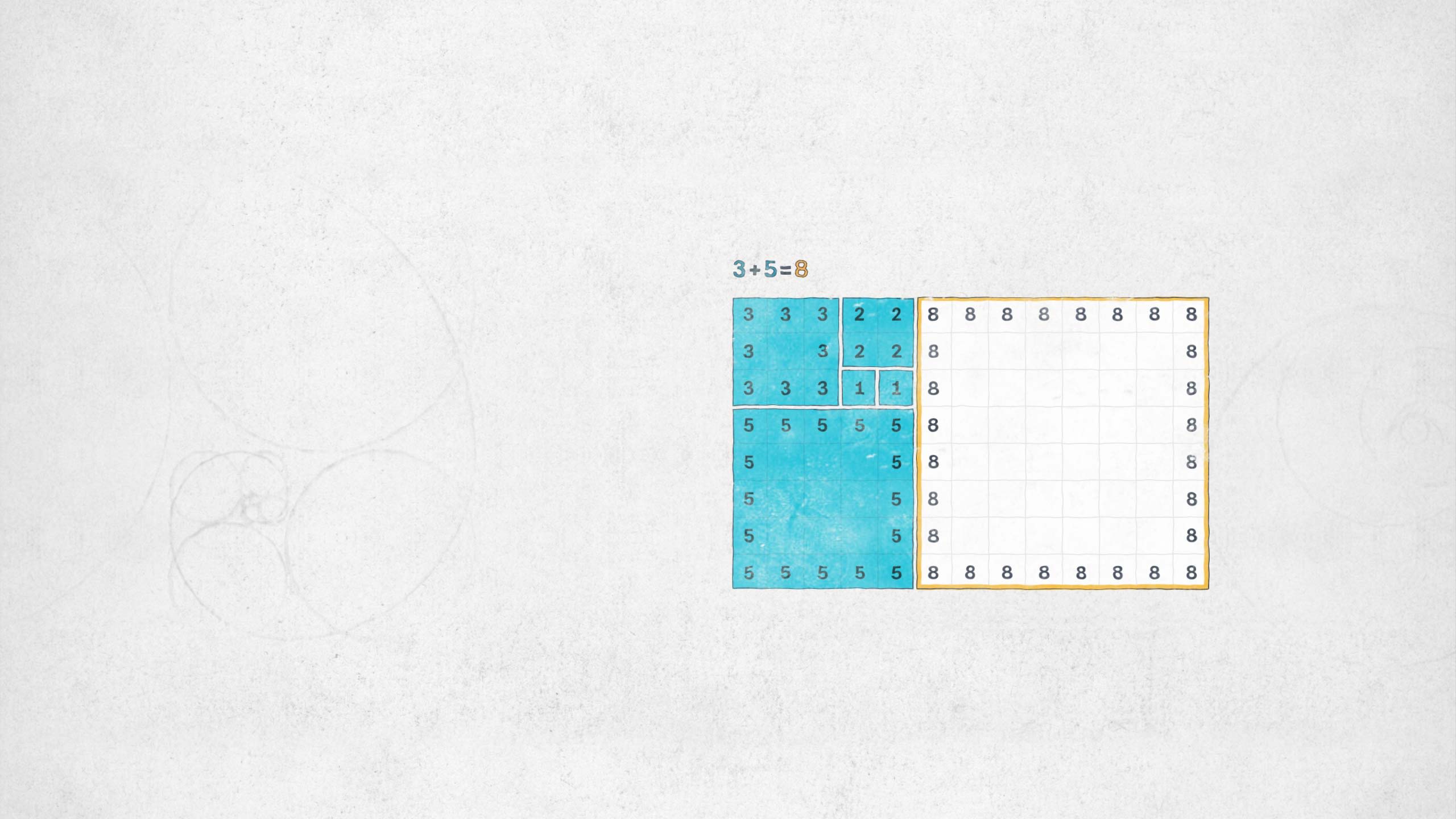
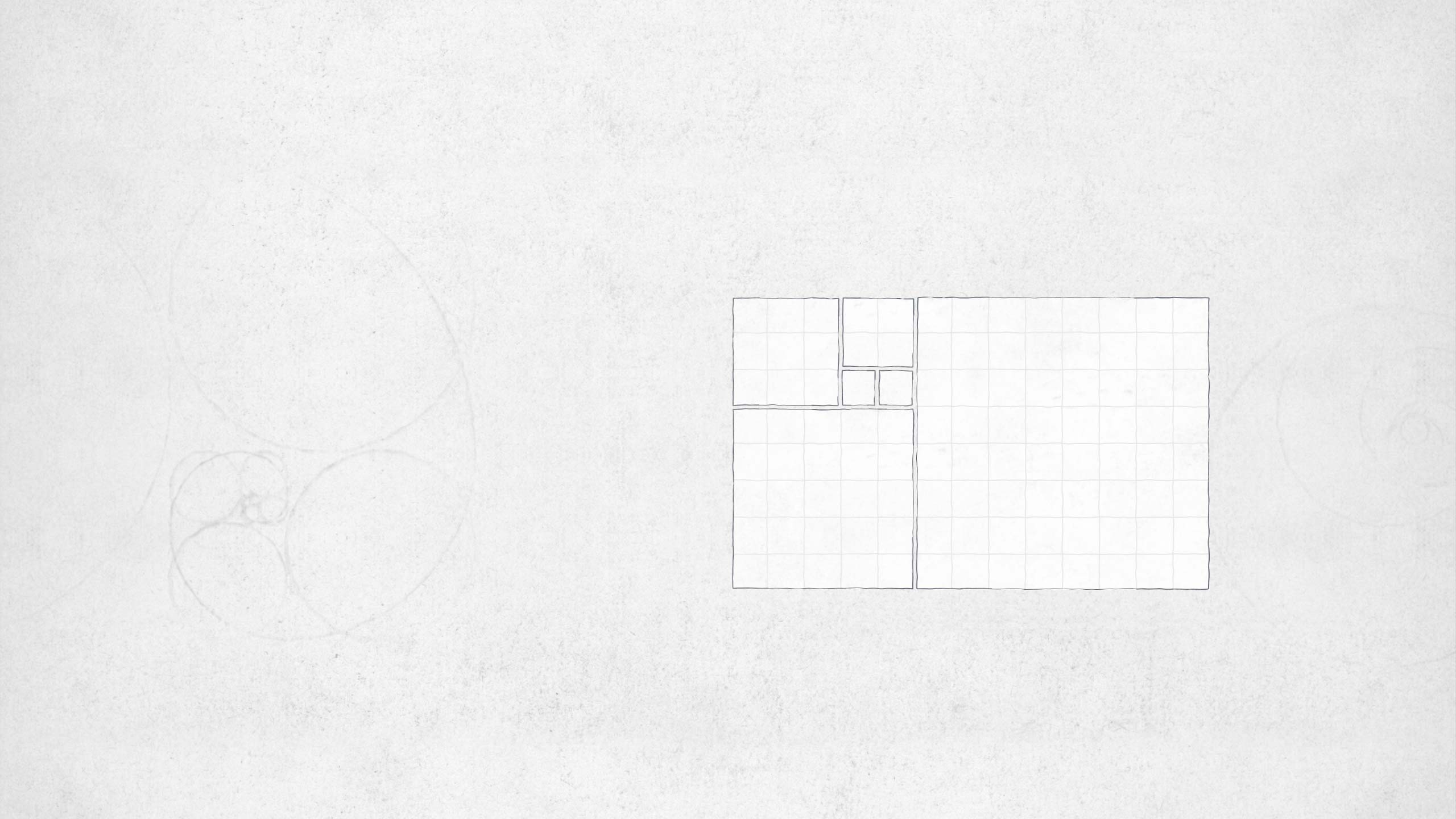




Die Fibonacci-Folge beschreibt viele Wachstumsvorgänge in der Natur und es scheint dabei eine Art Muster zu geben.
Es entsteht ein Muster, das unendlich weitergeführt werden kann.
Zieht man in den jeweiligen Rastern einen Halbkreis, entsteht ein uns sehr bekanntes Bild.
Diese perfekte Harmonie nutzen auch Künstler*innen, um Motive zu positionieren oder einen Blickpunkt zu wählen.
Das wohl bekannteste Beispiel: Leonardo da Vincis Mona Lisa.
Der Kreis




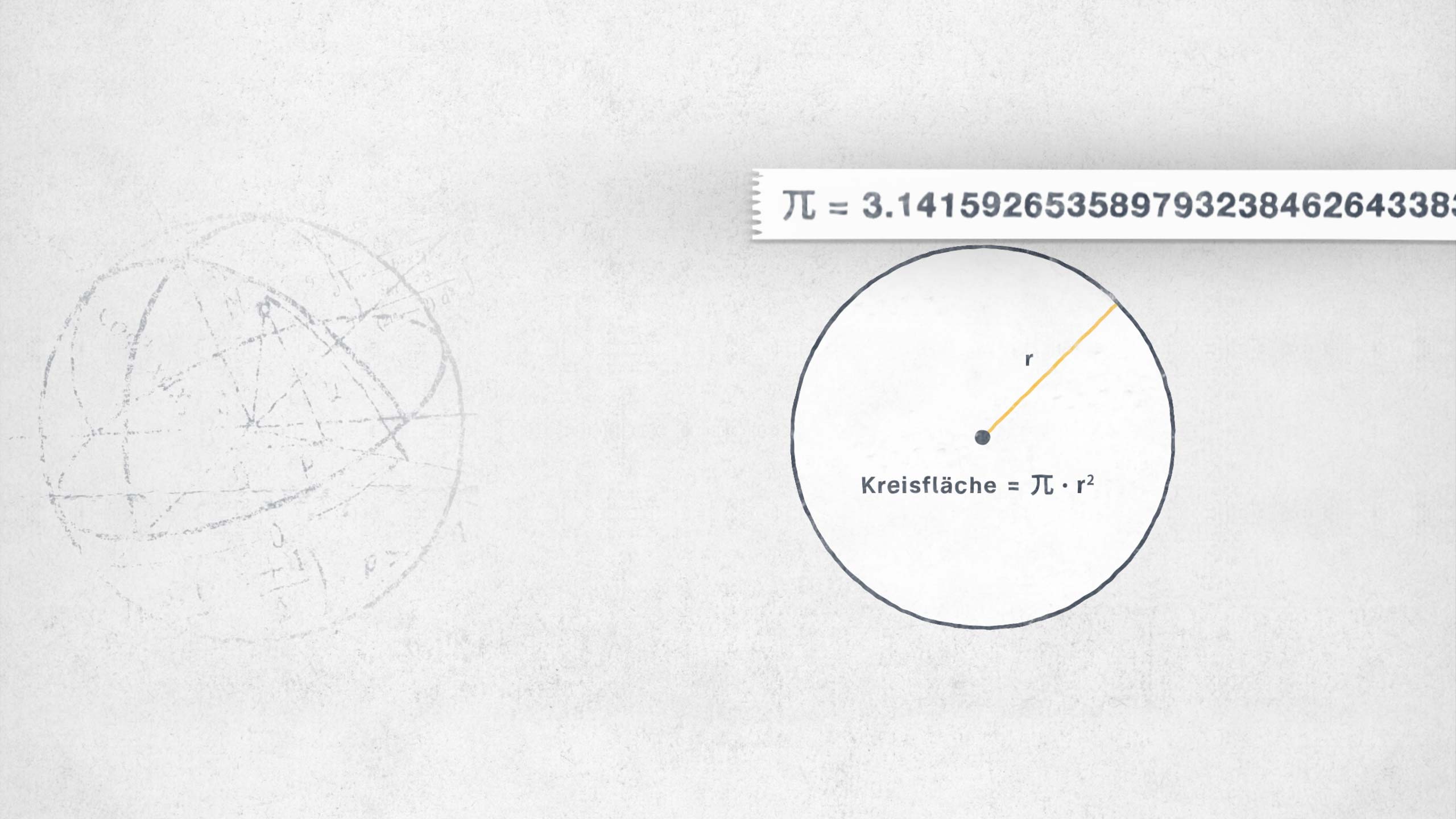
Kreise begegnen uns überall. In der Natur erfüllen sie meist einen bestimmten Zweck:
Sie speichern das Kostbare.
Und schützen das Empfindliche.
Als es den alten Ägypter*innen vor 3.500 Jahren zum ersten Mal gelang, den Kreis zu berechnen – dank der Annäherung an die Kreiszahl Pi – ermöglichte es ihnen, runde Silos als Getreidespeicher zu bauen. So konnte ihre Hochkultur erblühen.
Die Parabel
Sie ermöglicht den weitesten Weg bei geringstem Energieeinsatz. Und gilt für sämtliche Flugbahnen der Natur.


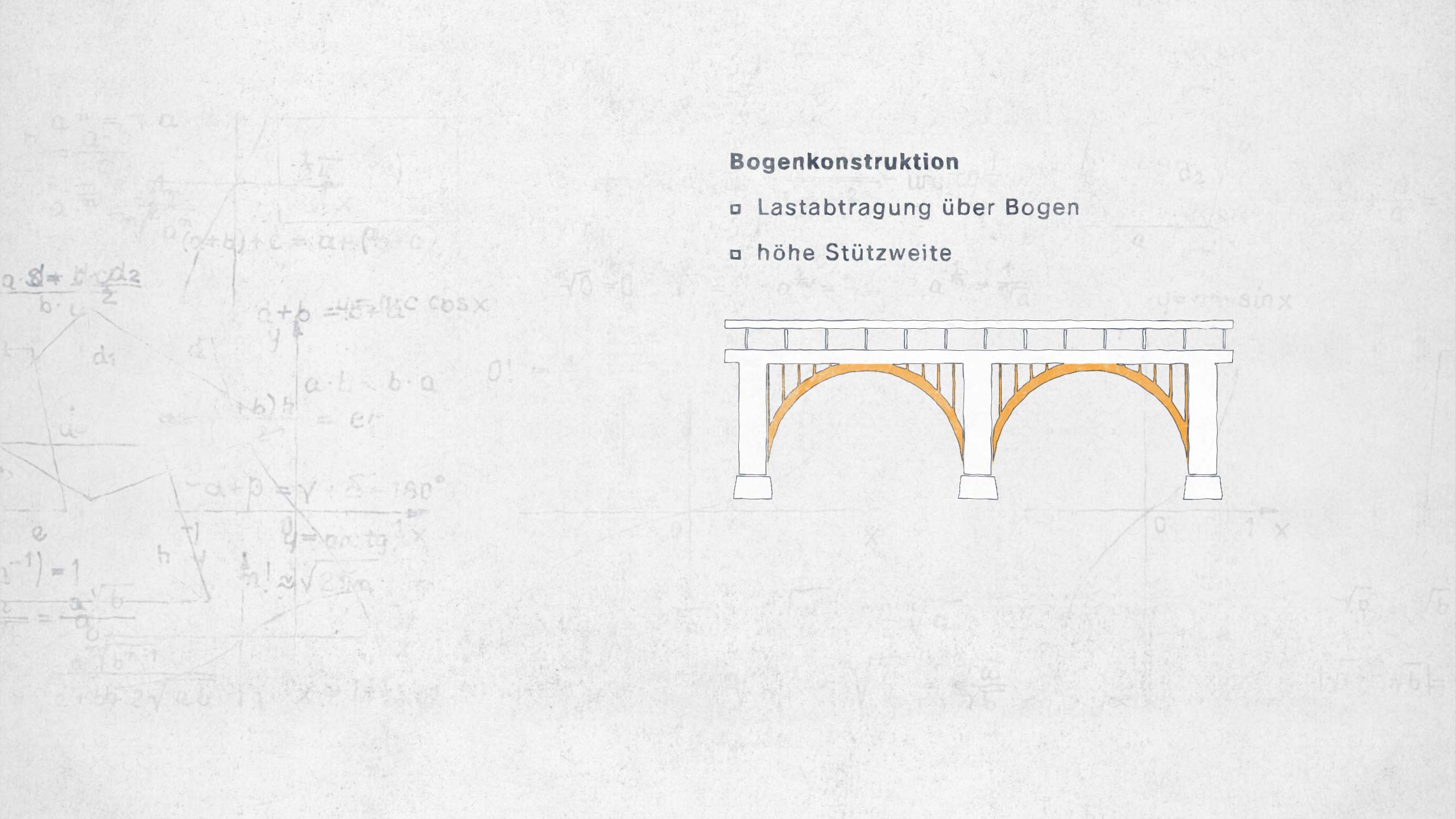
Die Parabel kann aber noch mehr. Sie bietet Stabilität – was sich Termiten bei ihren Bauten zu Nutze machen.
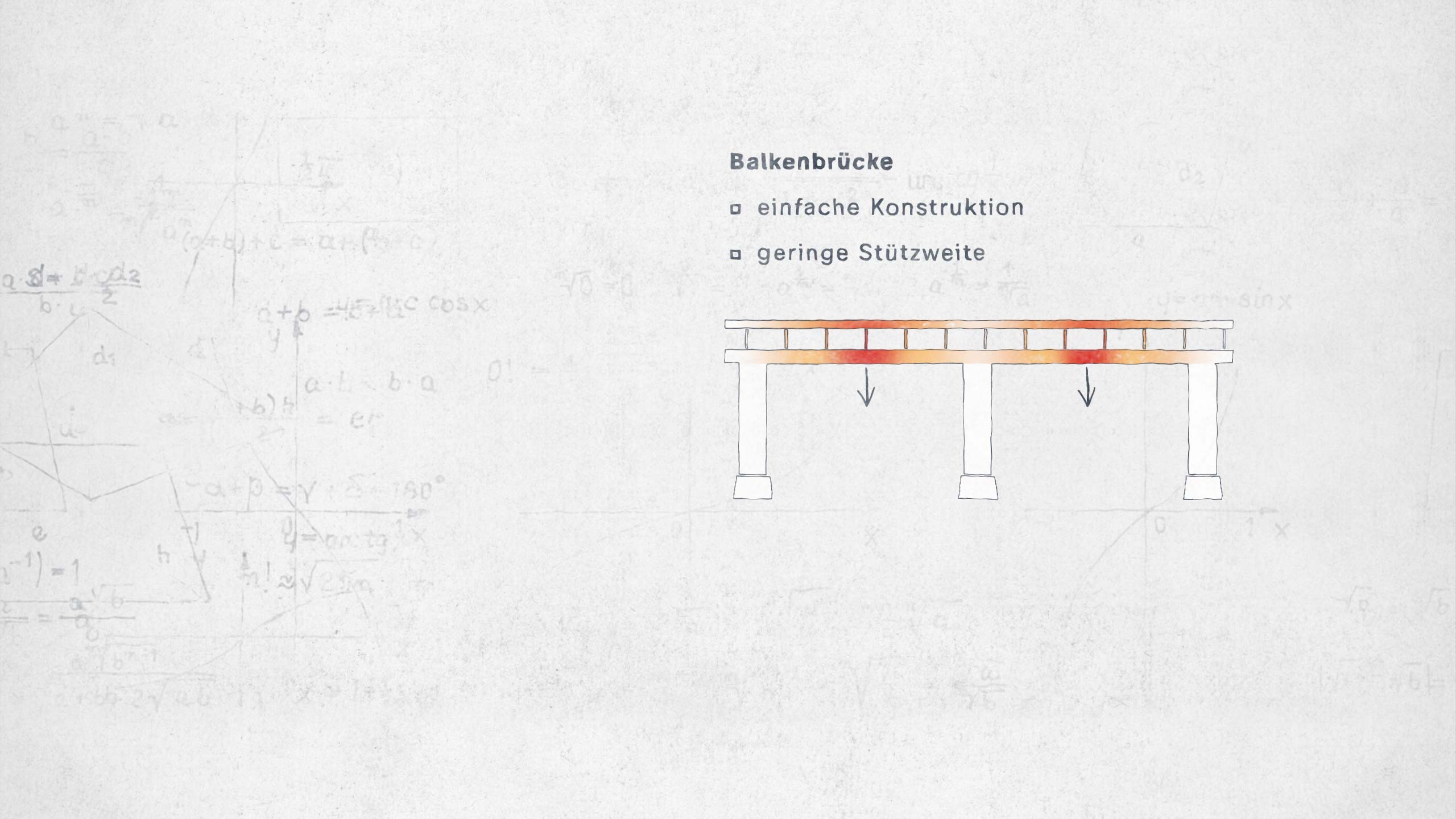
Dieses Wissen hat auch unser Bauwesen revolutioniert, zum Beispiel beim Brückenbau.
Das Hexagon
Bienen zeigen eine faszinierende Präzision in ihren Waben. Eine Fläche vollkommen gleichmäßiger Sechsecke.

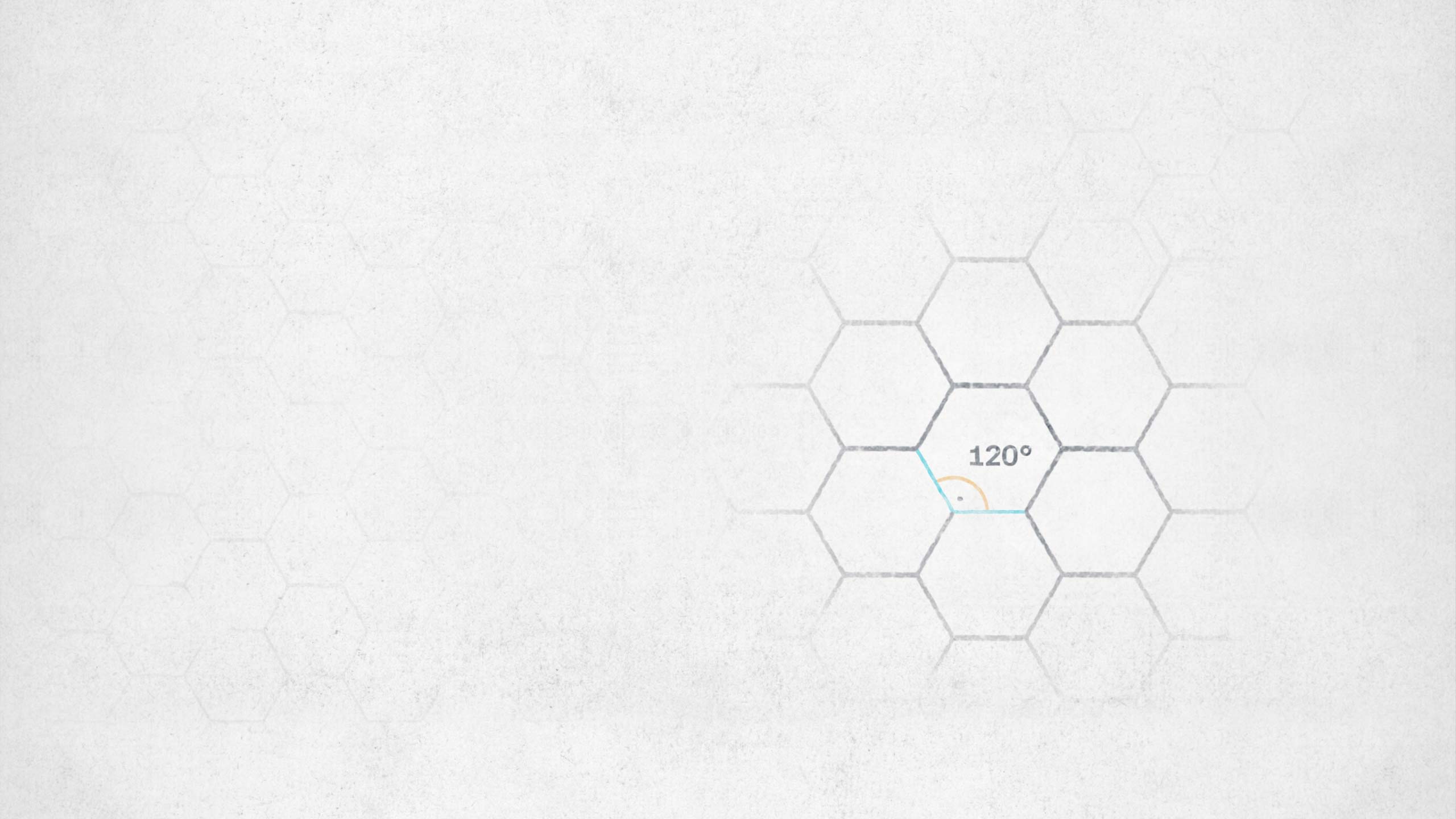


Würden sie den Kreis wählen, der zwar den größten Flächeninhalt von allen geschlossenen Formen besitzt, würden unnötige Zwischenräume entstehen.
Auch wir Menschen arbeiten an Möglichkeiten, das Bauwerk der Bienen zu kopieren – zum Beispiel im Autobau.
Dort könnte Stahlblech in Zukunft von Kunststoff-Waben ersetzt werden. Bei gleicher Größe sind die Waben leichter, aber doppelt so stabil. Unsere Autos würden nicht nur sicherer werden, sondern dank der Gewichtsreduzierung auch weniger Kraftstoff verbrauchen.
Die Formen und Formeln zu entschlüsseln ist kompliziert, aber es lohnt sich.
Denn immer, wenn das in der Geschichte gelungen ist, war das ein Garant für Fortschritt.


Quellen:
Brandenburgische Technische Universität Cottbus; Späth-Arboretum der Humboldt-Universität; Fakultät für Biologie, Universität Freiburg; Georg Glaeser: Der mathematische Werkzeugkasten; Károly Somonyi: Kultur Geschichte der Physik – Von den Anfängen bis heute; Sander Bais: Die Gleichungen der Physik – Meilensteine des Wissens; Josef Honerkamp: Die Entdeckungen des Unvorstellbaren – Einblicke in die Physik und ihre Methode; Hans Wußing: 6.000 Jahre Mathematik – eine kulturgeschichtliche Zeitreise
Fotos:
Pond5; Getty Images; Adobe Stock; Nadine Moeller, Gregory Marouard, Tell Edfu Project; iStock; ZDF
Autorin:
Jennifer Werner
Redaktion:
Katharina Kohl, Karsten Kaminski
Im Auftrag des ZDF:
Design:
Mischa Biekehör